on trying to figure out i^i, I stumbled on the following fallacy that I can not peg:
1 = 1
(-1)(-1) = (1) (1)
(-1)^2 = (1)^2
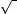 (-1)^2 =
(-1)^2 =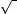 (1)^2
(1)^2
(-1)^(2 * 1/2) = (1) ^(2 * 1/2)
(-1)^1 = (1) ^ 1
-1 = 1 QED
hum.
on trying to figure out i^i, I stumbled on the following fallacy that I can not peg:
1 = 1
(-1)(-1) = (1) (1)
(-1)^2 = (1)^2
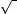 (-1)^2 =
(-1)^2 =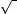 (1)^2
(1)^2
(-1)^(2 * 1/2) = (1) ^(2 * 1/2)
(-1)^1 = (1) ^ 1
-1 = 1 QED
hum.
The square root has two solutions. So this line:
(-1)^1 = (1) ^ 1
would better be expressed as:
(-1)^1 = ±(1) ^ 1
leaving you with
-1 = ±1
and the time to ponder a different mystery instead.
I think you got it, thank you.
-brewster
Brewster,
Were you just being coy? Maybe an odd choice of word. But somehow
I get a flirtation from someone who is quite clever.
The funny thing is I wouldn’t of got the answer immediately 25 years ago.
(Guess I am not a particularly fast learner.)
Here is another puzzle. What does it mean to get a real number uniformly
distributed from 0 to 1 on a digital computer? Another question which
involves the domain of number we are working within.
Hank, hope you are doing well. Thanks for writing something down.
-Kirk
I stumbled over the same puzzle 20 years ago and asked my Math teacher. He was puzzled, too and took the mystery home. The next week, he presented me with the solution:
Taking the square root of a negative number isn’t defined using the rules from rational numbers. You have to switch to the rules of irrational numbers. So as soon as you write the root symbol on the left side, you have different number systems on each side of the equals which makes the equals wrong.
So the fourth equals sign is wrong. It doesn’t matter that you never actually take the negative root. If you want to stay in the rational numbers, you can’t write sqrt(-1).
See also Notes at the end of http://en.wikipedia.org/wiki/Square_root#Square_roots_of_negative_and_complex_numbers